这篇文章上次修改于 1464 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

笛卡尔心形函数，心形线，是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹，因其形状像心形而得名。那天，偶然认识到了这个被修改过的笛卡尔函数。

函数体

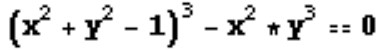
在数学绘图软件中

代码 & 解析

//alphaae 180509
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main(int argc, char* argv[]) {
    system("title");
    double x, y, f;
    //利用for循环构建一个 y 在 -1.1 到 1.4，x 在 -1.5 到 1.5 的平面
    //并且以固定精度扫描每一个点
    for (y = 1.4; y > -1.1; y -= 0.1) {
        for (x = -1.5; x < 1.5; x += 0.045) {
            //笛卡尔心形函数 即 (x^2 + y^2 -1) - x^2 * y^3 = 0
            f = pow(pow(x, 2) + pow(y, 2) - 1, 3) - pow(x, 2) * pow(y, 3);
            if (f <= 0.0) {        //小于等于0，即为在函数内的点
                printf("*");
            }
            else {
                printf(" ");
            }
        }
        printf("\n");
    }
    system("pause>nul");
    return 0;
}

import numpy

# 利用for循环构建一个 y 在 -1.1 到 1.4，x 在 -1.5 到 1.5 的平面
# 并且以固定精度扫描每一个点
for y in numpy.arange(1.4, -1.1, -0.1):
    for x in numpy.arange(-1.5, 1.5, 0.045):
        # 笛卡尔心形函数 即 (x^2 + y^2 -1) - x^2 * y^3 = 0
        f = pow(pow(x, 2) + pow(y, 2) - 1, 3) - pow(x, 2) * pow(y, 3)
        if (f <= 0.0):
            # 小于等于0，即为在函数内的点
            print("*", end='')
        else:
            print(" ", end='')
    print("")

结果